Arbeitsblatt: der peruanische Münzwurf
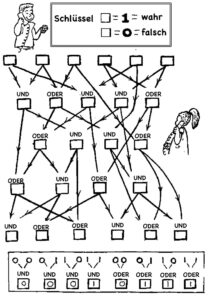
Wähle einige Eingaben für diesen Schaltkreis und ermittle, was die Ausgaben sind.
1. Ein offensichtliches Problem in der Praxis ist die Zusammenarbeit, die benötigt wird um einen Schaltkreis zu bauen, der für Alicia und Benito akzeptabel ist. Dies könnte die Aktivität für die Kinder unterhaltsam machen, aber es wird wahrscheinlich dazu führen, dass das Verfahren in der Praxis nicht funktioniert – besonders nicht am Telefon! Es gibt jedoch eine einfache Alternative, bei der Alicia und Benito ihre Schaltkreise unabhängig voneinander konstruieren und öffentlich zugänglich machen können. Dann sendet Alicia ihre geheime Eingabe durch beide Schaltkreise und verbindet die beiden Ausgänge miteinander, indem sie die entsprechenden Bits vergleicht und die letzte Ausgabe zu einer Eins macht, wenn sie gleich sind und andernfalls zu Null setzt. In dieser Situation kann keiner der Teilnehmer schummeln, wenn der andere dies nicht tut, denn wenn nur eine der Schaltungen eine Einwegfunktion ist, dann ist die Kombination beider auch eine Einwegfunktion.
Die nächsten beiden Varianten betreffen nicht kryptographische Protokolle oder das Problem des Münzwerfens an sich, sondern eher das Konzept von Schaltkreisen, die aus UND und ODER-Gattern aufgebaut sind. Es werden einige wichtige Begriffe der Grundlagen erklärt, die sich nicht nur der Computerschaltkreise, sondern auch der Logik selbst beziehen. Diese Art von Logik nennt man Boolesche Algebra, benannt nach dem Mathematiker George Boole (1815-64).
2. Die SchülerInnen mögen bemerkt haben, dass die Nur-Null-Eingabe 000000, es dazu gebracht hat, die Nur-Null-Ausgabe zu erzeugen, und ebenso wird durch den Nur-Eins-Input 111111 der Nur-Eins-Output erzeugt. (Es kann andere Eingaben geben, die diese Ausgaben ebenfalls erzeugen; tatsächlich gibt es für den Beispielschaltkreis-000010 nur Nullen, während 110111 nur Einsen erzeugt.)
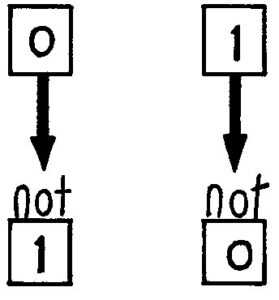 Dies folgt aus der Tatsache, dass die Schaltkreise nur aus UND- und ODER-Gattern bestehen. Durch Hinzufügen eines NICHT-Gatters, das nur eine Eingabe benötigt und die Umkehrung als Ausgabe erzeugt (d. h. 0 •1 und 1 → 0), können die SchülerInnen Schaltkreise konstruieren, die diese Eigenschaft nicht haben.
Dies folgt aus der Tatsache, dass die Schaltkreise nur aus UND- und ODER-Gattern bestehen. Durch Hinzufügen eines NICHT-Gatters, das nur eine Eingabe benötigt und die Umkehrung als Ausgabe erzeugt (d. h. 0 •1 und 1 → 0), können die SchülerInnen Schaltkreise konstruieren, die diese Eigenschaft nicht haben.
3. Zwei andere wichtige Arten von Gattern sind UNDNICHT und ODER-NICHT (normalerweise abgekürzt als NAND und NOR), die gleich sind wie UND und ODER, die Ausgabe aber von einem NICHT umgekehrt wird.
Zum Beispiel ist ‚a UND-NICHT b’ dasselbe wie ‚NICHT (a UND b)’. Sie ermöglichen keine funktionell unterschiedlichen Schaltkreise, da deren Auswirkung immer mit dem entsprechenden UND- / ODER-Gatter, gefolgt von NICHT, erreicht werden kann. Interessant ist aber, dass alle anderen Gatter-Typen aus UND-NICHT-Gattern und ODER-NICHT-Gattern bestehen können.
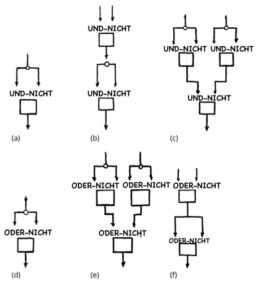
Nachdem UND-NICHT und ODER-NICHT den SchülerInnen vorgestellt wurden, fordere sie auf herauszufinden, ob eines dieser Gatter aus anderen miteinander verbundenen Gattern hergestellt werden kann. Dazu als weiteren Schritt, ob solche Gatter auch aus nur einem Typ von miteinander verbundenen Gattern hergestellt werden kann. Die folgende Abbildung zeigt, wie die drei grundlegenden Gatter NICHT, UND und ODER aus UND-NICHT-Gattern in der oberen Reihe und ODER-NICHT-Gattern in der unteren Reihe konstruiert werden können.
Laden Sie hier das Arbeitsblatt im PDF-Format herunter.
