Aktivität 9 – Minimale Spannbäume
Die Schlammstadt – Minimale Spannbäume
Unsere Gesellschaft ist durch mehrere Netzwerke verbunden: Telefonnetze, Versorgungsnetze, Computernetze und Straßennetze. Für ein bestimmtes Netzwerk gibt es in der Regel eine gewisse Auswahl, wo die Straßen, Kabel oder Funkverbindungen platziert werden können. Wir müssen Wege finden, um Objekte in einem Netzwerk effizient zu verbinden.
- Problemlösung
- 9+
Worum geht es in dieser Aktivität?
Angenommen du entwirfst einen Plan, wie die Versorgung von Strom, Gas oder Wasser zu einem neuen Haus sichergestellt werden soll. Ein Netz von Drähten oder Rohren wird benötigt, um alle Häuser mit dem entsprechenden Dienstleistungsunternehmen zu verbinden. Jedes Haus muss mit dem Netzwerk an einer Stelle verbunden sein, aber der Weg, der die Dienstleistung zu dem betroffenen Haus bringt, spielt keine wesentliche Rolle, solange der Anschluss existiert.
Die Aufgabe, ein Netz mit einer minimalen Gesamtlänge zu entwerfen, heißt das minimale Spannbaum-Problem.
Minimale Spannbäume sind nicht nur in Gas- und Stromnetzen nützlich; sie helfen auch Probleme in Computernetzwerken, Telefonnetzwerken, Ölpipelines und für Fluglinien zu lösen. Allerdings muss bei einer Entscheidung für eine Reise über die beste Route, vom Anbieter berücksichtigt werden, wie angenehm die Reise für die Reisenden ist und wie viel es kosten wird. Niemand will Stunden in einem Flugzeug verbringen, das einen langen Umweg in ein anderes Land wählt, nur weil es billiger ist. Der Schlammstadt-Algorithmus kann für diese Netzwerke nicht viel genutzt werden, da er hier nur die Gesamtlänge der Straßen oder Flugwege minimiert.
Minimale Spannbäume sind auch als einer der Lösungsschritte anderer Graphenprobleme, wie für das ‘Problem des Handlungsreisenden’ (Travelling Salesman Problem, TSP) nützlich, wo versucht wird den kürzesten Weg zu finden, der jeden Punkt im Netzwerk beinhaltet.
Es gibt effiziente Algorithmen (Methoden) zur Lösung minimaler Spannbaum-Probleme. Eine einfache Methode für eine optimale Lösung ist Kruskals Algorithmus (J.B. Kruskal, publiziert 1956): Beginne mit einem Punkt (Knoten) des Graphen und füge Linien (Kanten) in zunehmender Reihenfolge der Größe hinzu, wenn dadurch ein weiterer Teil des Netzwerks hinzukommt, der noch nicht mit dem Graphen verbunden ist.
Für viele Graphenprobleme, einschließlich TSP, haben InformatikerInnen noch keine schnelle Methode entdeckt, um dadurch die besten möglichen Lösungen zu finden.
Arbeitsblatt: Das Schlammstadt-Problem
Es gab einmal eine Stadt, in der es keine Straßen gab. Die Stadt zu erkunden war besonders nach Regenfällen schwierig, weil der Boden sehr schlammig wurde - Autos steckten im Schlamm fest und die Leute bekamen dreckige Stiefel. Der Bürgermeister der Stadt entschied, dass einige der Straßen gepflastert werden sollten, aber nicht mehr Geld als nötig dafür ausgegeben werden sollte, weil die Stadt auch vorhatte, ein Schwimmbad zu bauen. Der Bürgermeister gab daher zwei Bedingungen an:
1. Genug Straßen müssen gepflastert werden, sodass es für jeden möglich ist, von seinem Haus aus nur auf gepflasterten Straßen zu jedem anderen Haus gehen zu können und
2. das Pflastern sollte so wenig wie möglich kosten.
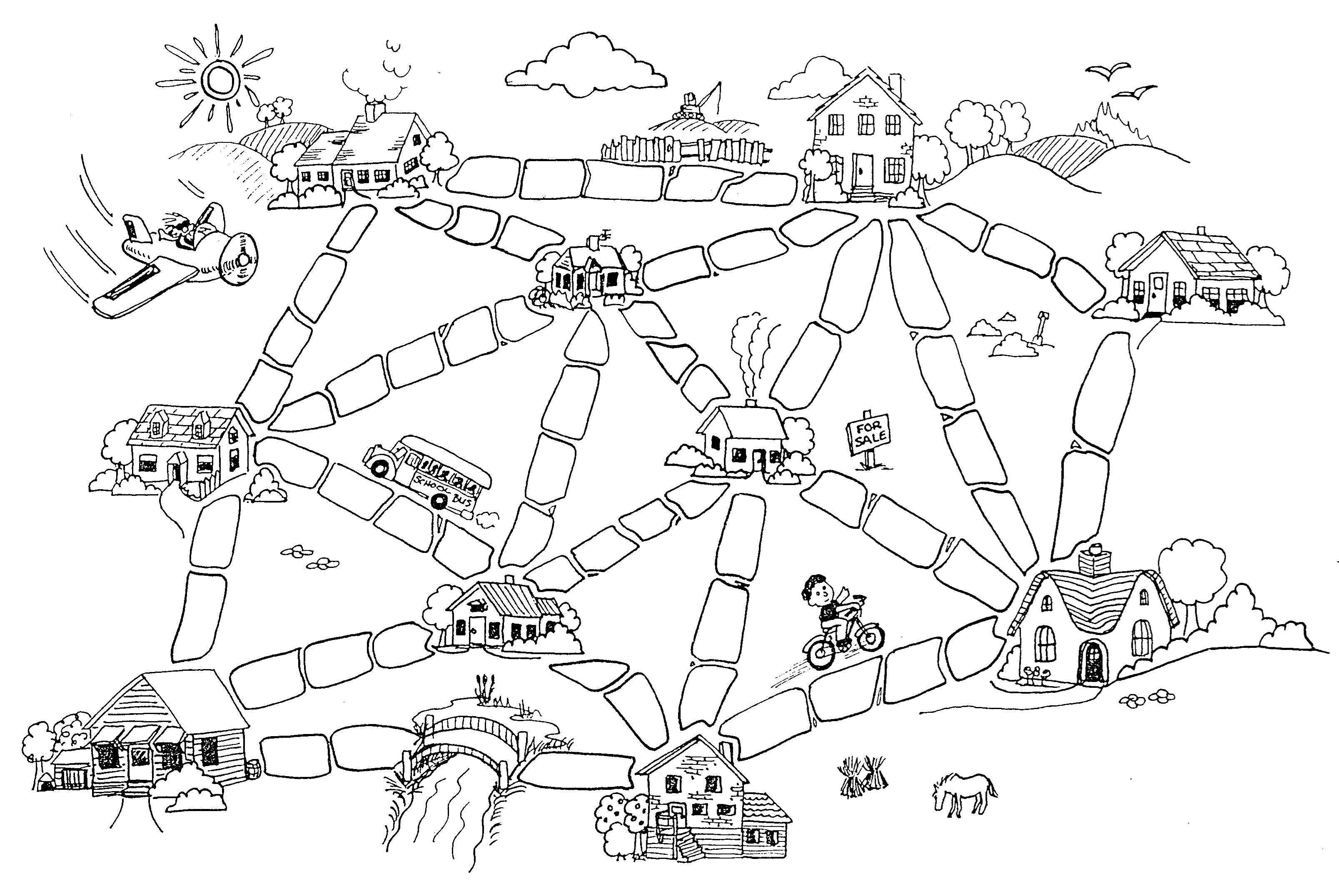
Unten ist der Grundriss der Stadt dargestellt. Die Anzahl der Pflastersteine zwischen jedem Haus stellt die Kosten für die Pflasterung dieser Strecke dar. Finde die beste Route, die alle Häuser verbindet, aber bei der du so wenig Spielmarken (Pflastersteine) wie möglich benutzen musst.
Welche Strategien hast du zur Lösung des Problems benutzt?
Variationen und Erweiterungen
Hier ist eine andere Möglichkeit zur Darstellung von Städten und Straßen:
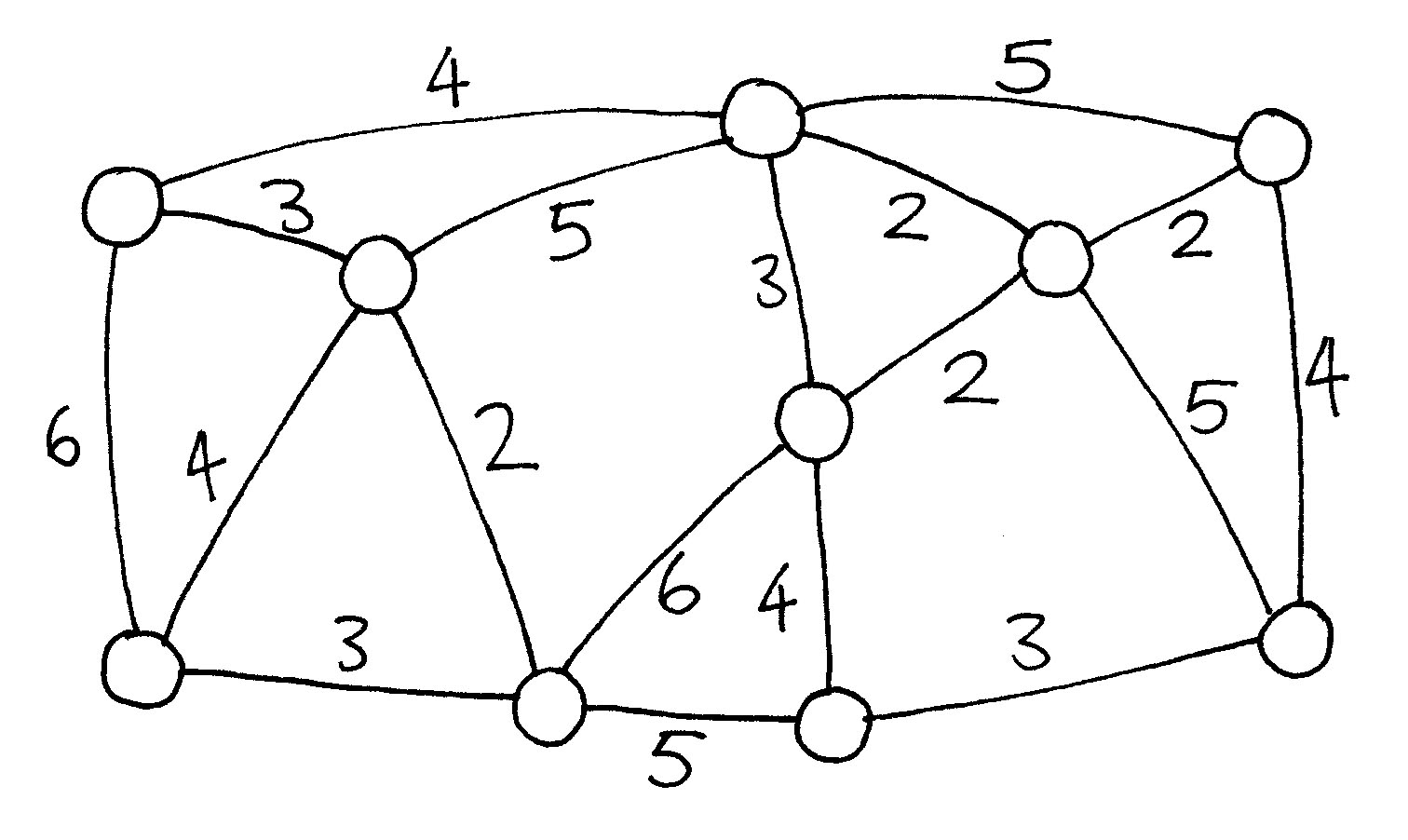
Die Häuser werden durch Kreise (oder Punkte), die schlammigen Straßen durch Linien und die Länge einer Straße wird durch die Zahl an der entsprechenden Linie dargestellt.
InformatikerInnen und MathematikerInnen benutzen diese grafische Abbildung oft zur Darstellung des Problems; sie nennen es einen Graphen. Das kann verwirren, weil ein „Graph“ in der Statistik manchmal als ein Diagramm zur Darstellung numerischer Daten, wie z.B. das Balkendiagramm, verwendet wird. Graphen in der Informatik werden aber nicht so verstanden; die Länge muss nicht maßstäblich gezeichnet werden.
Folge einigen schwierigen Wegen auf den gepflasterten Straßen deines eigenen Graphen und probiere diese Wege auch auf den Graphen deiner Freunde.
Findest du eine Regel um zu beschreiben, wie viele Straßen oder Verbindungen für eine beste Lösung notwendig sind? Ist das abhängig von der Anzahl der Häuser in der Stadt?
Materialien
- Arbeitsblatt: Das Schlammstadt-Problem
- Spielmarken oder Quadrate aus Karton (ungefähr 40 pro SchülerIn)