Aktivität 8 – Sortiernetzwerk
Schneller fertig sein –Sortiernetzwerk
Obwohl Computer schnell sind, gibt es Grenzen, wie schnell sie Probleme lösen können. Eine Möglichkeit, Dinge zu beschleunigen, ist mehrere Computer zu verwenden um verschiedene Teile eines Problems zu lösen. In dieser Aktivität verwenden wir Sortiernetzwerke, die mehrere Sortiervergleiche gleichzeitig ausführen.
Mathematik: Einführung von Zahlen – Zahlen vergleichen: ‘größer als’, ‘kleiner als’
- Vergleiche
- Ordnen
- Gemeinsame Problemlösung
7+
Worum geht es in dieser Aktivität?
Da wir Computer immer häufiger verwenden, möchten wir, dass sie Informationen so schnell wie möglich verarbeiten.
Eine Möglichkeit Computer zu beschleunigen ist es, Programme zu schreiben, die weniger Rechenschritte ausführen (das wurde in den Aktivitäten Suchalgorithmen und Sortieralgorithmen gezeigt).
Eine andere Möglichkeit, Probleme schneller zu lösen, ist es mehrere Computer zu verwenden, die verschiedene Teile derselben Aufgabe gleichzeitig bearbeiten. Zum Beispiel das Sechs-Zahlen-Sortiernetzwerk: Obwohl insgesamt 12 Vergleiche zur Sortierung notwendig sind, können bis zu drei davon gleichzeitig ausgeführt werden. Das bedeutet, dass insgesamt nur die Zeit für fünf Vergleichsschritte benötigt wird. Dieses Parallelnetzwerk sortiert die Liste mehr als doppelt so schnell wie ein System, das pro Schritt nur einen Vergleich durchführen kann.
Nicht alle Aufgaben können durch Parallelverarbeitung schneller erledigt werden. Als Analogie dazu stellen Sie sich vor, eine Person gräbt einen zehn Meter langen Graben. Wenn zehn Personen jeweils einen Meter des Grabens ausgraben würden, könnte die Aufgabe viel schneller erledigt werden. Jedoch könnte die gleiche Strategie nicht auf einen Graben angewendet werden, der zehn Meter tief sein soll - der zweite Meter ist nicht zugänglich, bis der erste Meter ausgegraben worden ist. ComputerwissenschaftlerInnen sind ständig dabei, die besten Wege zu suchen, um solche Probleme durch Computer mithilfe von Parallelverarbeitung zu lösen.
Materialien
- Kreide
- Zwei Sätze mit je sechs Blättern. Originalkopie ,Sortiernetzwerk’ auf Blatt drucken und ausschneiden
- Stoppuhr
Übung: Sortiernetzwerke
Vor der Aktivität: Benutze die Kreide und male dieses Netzwerk auf den Boden.
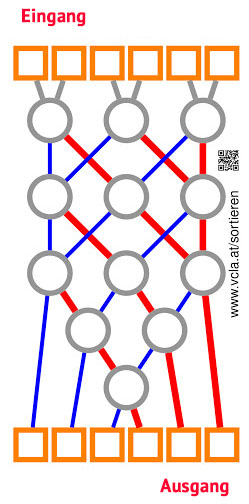
Diese Aktivität wird euch zeigen, wie Computer unter Verwendung des sogenannten Sortiernetzwerks, zufällig gewählte Zahlen ordnen.
-Teilt euch in Gruppen mit jeweils sechs Mitgliedern auf. Nur eine Gruppe wird jeweils das Netzwerk verwenden.
-Jedes Teammitglied wählt ein nummeriertes Blatt (Originalkopie ,Sortiernetzwerk’).
-Jedes Teammitglied positioniert sich in einem der Startpunkte (Quadrate) auf der linken Seite – markiert durch ‘Eingang’. Eure Zahlen sollen ungeordnet verteilt sein.
-Geht die markierten Linien entlang und wartet auf jemanden, wenn ihr einen Kreis erreicht habt.
-Wenn ein anderes Teammitglied in eurem Kreis ankommt, vergleicht eure Blätter. Derjenige von euch mit der kleineren Zahl verlässt den Kreis nach links; der mit der größeren Zahl benutzt die Abzweigung nach rechts.
-Seid ihr in der richtigen Reihenfolge, wenn ihr an das andere Ende des Feldes ankommt?
Falls ein Team einen Fehler macht, beginnt das Team nochmals von vorn. Prüft, ob ihr die Ausführung der Regel in den Kreisen verstanden habt und bei kleineren Zahlen den linken Weg, sowie bei größeren Zahlen den rechten Weg genommen habt.
Falls ein Team einen Fehler macht, beginnt das Team nochmals von vorn. Prüft, ob ihr die Ausführung der Regel in den Kreisen verstanden habt und bei kleineren Zahlen den linken Weg, sowie bei größeren Zahlen den rechten Weg genommen habt. Hier ein Beispiel:
- Wenn die SchülerInnen mit dieser Aktivität vertraut sind, verwende eine Stoppuhr, um zu messen wie lang jedes Team braucht um durch das Netzwerk zu kommen.
- Verwende Blätter mit größeren Zahlen (z.B. die dreistelligen Zahlen auf der Originalkopie ,Sortiernetzwerk’).
- Erstelle Blätter mit noch größeren Zahlen, um den Aufwand beim Vergleich zu erhöhen oder benutze Wörter und vergleiche sie alphabetisch.
- Die Aktivität kann auch als Übung mit anderen Objekten verwendet werden, wie z.B. im Bereich Musik, wo Noten auf den Blättern aufgedruckt sind, die von der tiefsten zur höchsten oder von der kürzesten zur längsten Note sortiert werden sollen.
Weitere Aktivitäten
Die Zahlen werden in umgekehrter Reihenfolge sortiert.
Es wird nicht unbedingt funktionieren und die SchülerInnen sollten in der Lage sein, ein Beispiel für eine Eingabe zu finden, die in der falschen Reihenfolge herauskommt.
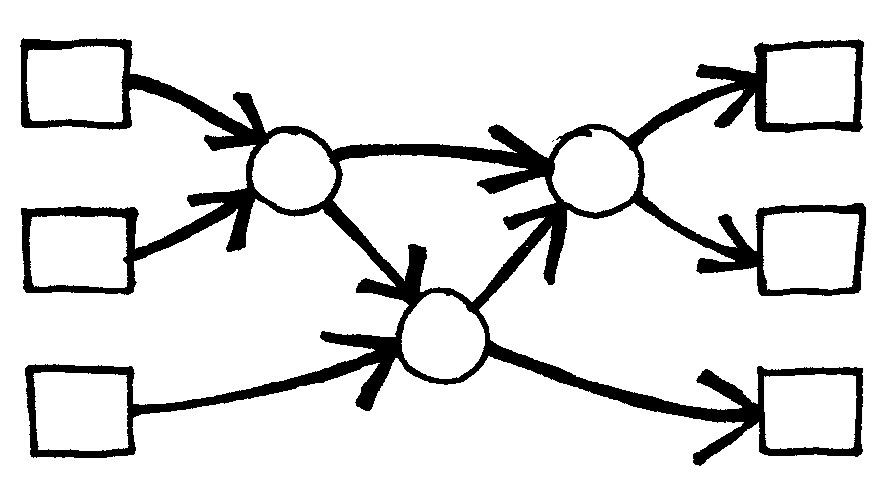
Das zweite ist schneller. Während beim ersten alle Vergleiche seriell (eins nach dem anderen) ausgeführt werden, wird es im zweiten Fall zum Teil gleichzeitig durchgeführt. Das erste Netzwerk ist ein Beispiel für eine serielle Verarbeitung, während im zweiten Fall Parallelverarbeitung verwendet wird, die schneller läuft.

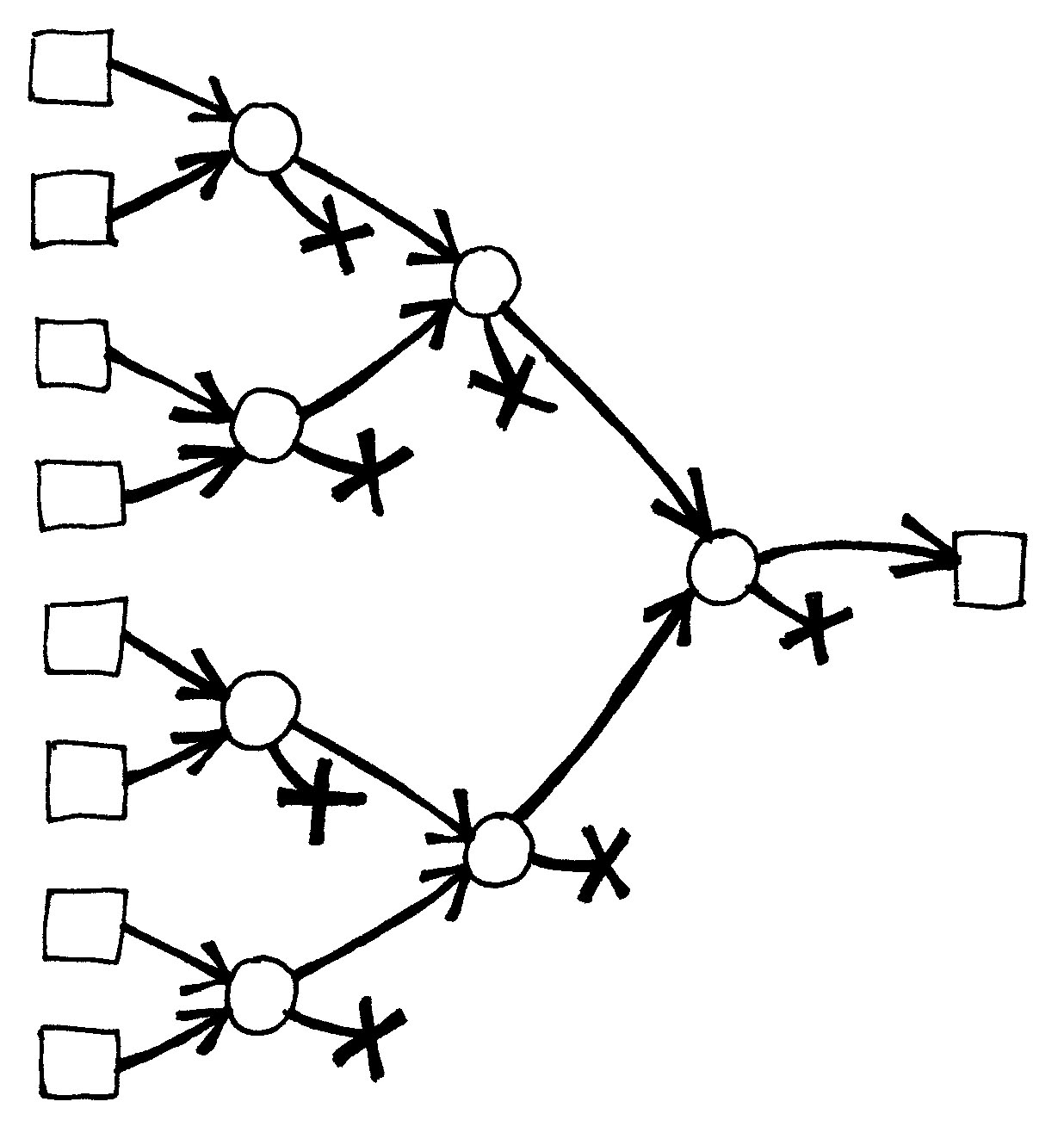
Netzwerke können auch verwendet werden, um minimale oder maximale Eingabewerte zu finden. Als Beispiel wird ein Netzwerk mit acht Eingaben gezeigt, dessen einziger Output dem minimalen Eingabewert entspricht (die anderen Eingabewerte werden in Sackgassen des Netzwerks abgelegt.)
Zum Beispiel wäre das Kochen eines Gerichtes viel langsamer, wenn man sich jeweils auf nur eine Beilage konzentriert und so alle Bestandteile des Gerichts erst nach und nach zubereitet werden. Können Aufträge schneller erledigt werden, wenn mehrere Personen angestellt werden? Bei welchen Aufträgen ist das nicht möglich?