Worum geht es in dieser Aktivität?

Das Problem mit der Karteneinfärbung, das wir in dieser Übung untersucht haben, besteht im Wesentlichen darin, die Mindestanzahl von Farben zu finden, die zum Ausmalen einer bestimmten Karte erforderlich sind - zwei, drei oder vier. Die Vermutung, dass jede Karte nur mit vier Farben gefärbt werden kann, wurde 1852 formuliert, aber erst 1976 bewiesen. Die Informatik ist voll ungelöster Probleme und zu wissen, dass das Vier-Farben-Theorem nach mehr als 120 Jahren Aufmerksamkeit von ForscherInnen bewiesen wurde, ist eine Ermutigung für diejenigen, die an anderen Problemen arbeiten, deren Lösung seit Jahrzehnten nicht gelungen ist.

Kartenfärbung gehört zu einer allgemeinen Klasse von Problemen, in der Graphentheorie bekannt als „Färbung“. In der Informatik ist ein Graph eine abstrakte Darstellung von Beziehungen, wie hier gezeigt wird.

Wie in Aktivität 9 über die Schlammstadt erwähnt, wird der Begriff ‚Graph’ in der Mathematik in einer anderen Bedeutung verwendet, um ein Diagramm zu bezeichnen, das numerische Daten wie ein Balkendiagramm anzeigt. Aber die Graphen, die InformatikerInnen benutzen, stehen damit nicht in Zusammenhang. In der Informatik werden Graphen mit Kreisen oder großen Punkten gezeichnet, die technisch „Knoten“ genannt werden, um Objekte zu bezeichnen, wobei Linien zwischen ihnen eine Art von Beziehung zwischen den Objekten anzeigen.

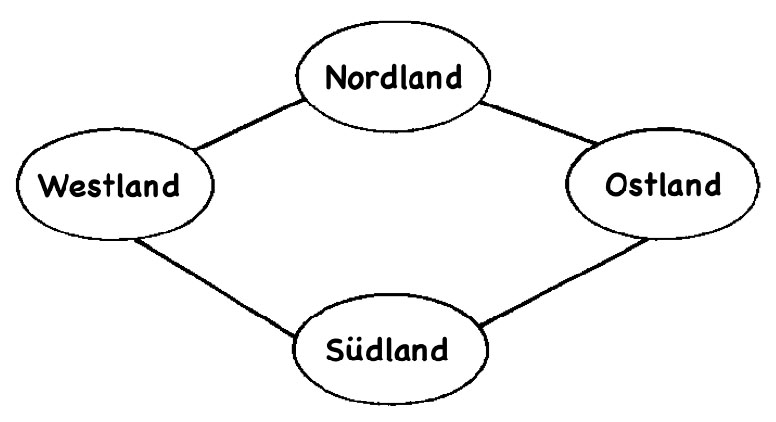
Der obige Graph stellt die Karte am Anfang dieser Aktivität dar. Die Knoten repräsentieren die Länder und eine Linie zwischen zwei Knoten zeigt an, dass diese beiden Länder eine gemeinsame Grenze haben. In der Graphentheorie bedeutet die Farbregel, dass keinem Nachbarknoten die gleiche Farbe zugewiesen werden soll. Anders als bei einer Karte gibt es keine Begrenzung für die Anzahl der Farben, die ein allgemeiner Graph benötigen könnte, da viele verschiedene Beschränkungen als Verbindungslinien eingezeichnet werden können, während die zweidimensionale Natur von Karten die möglichen Anordnungen einschränkt. Das „Graphenfärbung-Problem“ besteht darin, die minimale Anzahl von Farben zu finden, die für einen bestimmten Graphen benötigt werden.

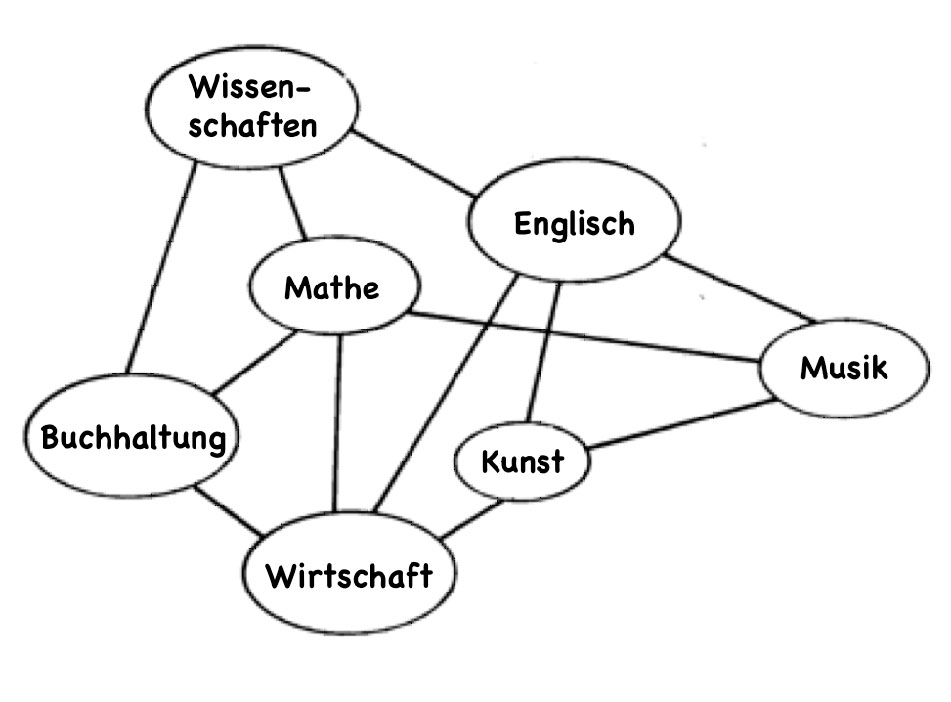
Die Knoten in dem Graphen rechts beziehen sich auf Schulfächer. Eine Linie zwischen zwei Fächern zeigt an, dass mindestens ein Schulkind beide Fächer belegt und daher nicht für denselben Zeitraum geplant werden sollte. Unter Verwendung dieser Darstellung entspricht das Problem, einen funktionsfähigen Stundenplan unter Verwendung der minimalen Anzahl von Perioden zu finden, dem Färbungsproblem, bei dem die verschiedenen Farben unterschiedlichen Zeitbereichen entsprechen. Algorithmen zur Graphenfärbung sind von großem Interesse in der Informatik und werden für viele reale Probleme verwendet, obwohl sie wahrscheinlich nie zum Einfärben von Karten verwendet werden - unser armer Kartograph ist nur eine Fiktion!

Es gibt buchstäblich Tausende andere Probleme, die auf Graphentheorie basieren. Einige werden an anderer Stelle in diesem Buch beschrieben, wie der minimal spannende Baum von Aktivität 9 und die Dominating Sets von Aktivität 15. Graphen sind eine sehr allgemeine Art der Darstellung von Daten und können verwendet werden, um alle Arten von Situationen darzustellen, wie zum Beispiel eine Karte aus Straßen und Kreuzungen, Verbindungen zwischen Atomen in einem Molekül, Pfade, die Nachrichten über ein Computernetzwerk aufnehmen können, Verbindungen zwischen Komponenten auf einer Leiterplatine und Beziehungen zwischen den Aufgaben, die zur Durchführung eines großen Projekts erforderlich sind. Aus diesem Grund haben Probleme mit Graphendarstellungen die InformatikerInnen seit langem fasziniert. Viele dieser Probleme sind konzeptionell nicht schwierig, aber sehr schwierig, weil sie lange brauchen, um gelöst zu werden. Zum Beispiel könnte ein Computer zur Bestimmung der effizientesten
Lösung für ein Graphenfärbungsproblem von mäßiger Größe - wie zum Beispiel die Suche nach dem besten Weg, eine Schule mit dreißig Lehrern und 800 Schülern zu planen - Jahre oder sogar Jahrhunderte dauern, obwohl er den bekanntesten Algorithmus verwendet. Das Problem wäre irrelevant zu dem Zeitpunkt, bei dem die Lösung gefunden wurde, und zwar unter der Annahme, dass der Computer nicht kaputt geht oder abgenutzt wird, bevor er damit fertig ist! Solche Probleme werden nur in der Praxis gelöst, weil wir uns mit suboptimalen, aber immer noch sehr guten Lösungen zufrieden geben. Wenn wir darauf bestehen würden, die gefundene Lösung als die beste zu garantieren, wäre das Problem völlig unlösbar. Die Menge an Computerzeit, die zur Lösung von Farbproblemen benötigt wird, steigt exponentiell mit der Größe des Graphen. Betrachten wir das Problem mit der Karteneinfärbung. Es kann gelöst werden, indem man alle möglichen Wege ausprobiert, um die Karte zu färben. Wir wissen, dass höchstens vier Farben benötigt werden, daher müssen wir jede Kombination der Zuordnung der vier Farben zu den Ländern bewerten. Da es n Länder gibt, gibt es 4n Kombinationen.

Diese Zahl wächst sehr schnell: Jedes Land, das hinzugefügt wird, multipliziert die Anzahl der Kombinationen mit vier und vervierfacht somit die Lösungszeit. Selbst wenn ein Computer erfunden würde, der das Problem für beispielsweise fünfzig Länder in nur einer Stunde lösen könnte, würde das Hinzufügen eines weiteren Landes vier Stunden erfordern, und wir müssten nur zehn weitere Länder hinzufügen, damit der Computer ein Jahr braucht um die Lösung zu finden. Diese Art von Problem wird nicht verschwinden, auch wenn wir immer schnellere Computer erfinden!

Die Färbung von Graphen ist ein gutes Beispiel für ein Problem, dessen Lösungszeit exponentiell zunimmt. Für sehr einfache Fälle des Problems, wie die kleine Anzahl von Karten, die in dieser Aktivität verwendet werden, ist es ziemlich einfach, die optimale Lösung zu finden, aber sobald die Anzahl der Länder über zehn steigt, wird das Problem sehr schwierig um von Hand zur Lösung zu kommen und mit 100 oder mehr Ländern kann sogar ein Computer viele Jahre brauchen, um alle möglichen Möglichkeiten auszuprobieren, um die optimale Lösung der Kartenfärbung zu finden.

Viele Probleme im wirklichen Leben sind von dieser Art, müssen aber trotzdem gelöst werden. InformatikerInnen verwenden auch Methoden, die gute, aber nicht perfekte Antworten geben. Diese heuristischen Techniken sind oft sehr nahe am Optimum, sehr schnell zu berechnen und geben Antworten, die für alle praktischen Zwecke nahe genug am Ziel sind. Schulen können es tolerieren, ein Klassenzimmer mehr zu benutzen als notwendig, wenn der Zeitplan perfekt wäre. Und vielleicht könnte sich der arme Kartograph eine zusätzliche Farbe leisten, obwohl es nicht unbedingt notwendig ist.

Niemand hat bewiesen, dass es keinen effizienten Weg gibt, um diese Art von Problemen auf herkömmlichen Computern zu lösen, ebenso hat bisher niemand das Gegenteil bewiesen und ComputerwissenschaftlerInnen sind skeptisch, dass jemals eine effiziente Methode gefunden werden kann. Wir werden in den nächsten beiden Aktivitäten mehr über diese Art von Problem erfahren.

Weiterführende Literatur

Harel diskutiert das Vier-Farben-Theorem einschließlich dessen Geschichte in Algorithmics. Weitere Aspekte des Kartenfärbungsproblems werden in Dies ist MEGA-Mathematik! von Casey und Fellows besprochen. Kubale’s 2004 erschienenes Buch Graph Colorings enthält eine Geschichte des Problems. Es gibt auch viele Internetseiten, die dieses Thema behandeln.