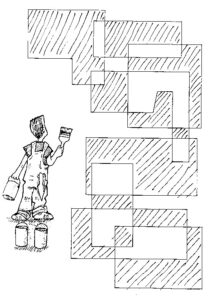
Arbeitsblatt: Bild einfärben 4
Färbe die Länder auf dieser Karte mit so wenigen Farben wie möglich, aber stelle sicher, dass keine zwei angrenzenden Länder die gleiche Farbe haben!
Variationen und Erweiterungen
Wie hier gezeigt, gibt es eine einfache Möglichkeit Karten zu erstellen, die nur zwei Farben benötigen. Diese Karte wurde gezeichnet, indem geschlossene Kurven (Linien, deren Anfang sich mit ihrem Ende verbindet) überlagert wurden.
Du kannst eine beliebige Anzahl dieser Kurven in beliebiger Form übereinander zeichnen, und erhältst immer eine Karte, die mit zwei Farben gefärbt werden kann. Die SchülerInnen können mit der Erstellung dieser Art von Karte experimentieren.
Vier Farben reichen immer aus, um eine Karte auf einem Blatt Papier oder auf einer Kugel (also einem Globus) zu zeichnen. Man könnte sich fragen (wozu Wissenschaftler ja bezahlt werden), wie viele Farben für Karten benötigt werden, die auf schrägen Oberflächen gezeichnet sind, wie zum Beispiel der Torus (die Form eines Donuts).
In diesem Fall braucht man fünf Farben, und fünf sind immer genug. Die SchülerInnen möchten vielleicht damit experimentieren.
Es gibt viele andere kurzweilige Varianten des Kartenfärbungsproblems, die in Richtungen führen, in denen vieles noch unbekannt ist.
Wenn ich zum Beispiel eine Karte auf einem Blatt Papier selbst male, weiß ich, dass vier Farben ausreichen, wenn ich clever arbeite. Aber angenommen, dass ich anstatt alleine zu arbeiten, mit einem inkompetenten (oder sogar gegnerisch gestimmten) Partner arbeite und wir wechseln uns ab, wenn wir die Farbe für Länder wählen. Angenommen, ich arbeite clever, während mein Partner
nur „korrekt“ arbeitet, wenn wir Länder auf der Karte färben. Wie viele Buntstifte müssen auf dem Tisch liegen, damit ich in meiner Klugheit die korrekten, aber nicht sehr schlauen (oder sogar subversiven) Schritte meines Partners wiedergutmachen kann?
Die maximale Anzahl ist nicht bekannt! 1992 wurde bewiesen, dass 33 Buntstifte immer genug sein werden und 2008 wurde durch einen Beweis gezeigt, dass 17 ausreichen würden, aber wir wissen immer noch nicht, dass diese vielen Schritte tatsächlich jemals benötigt werden. (Experten vermuten, dass weniger als 10 Farben ausreichen.)
Die SchülerInnen mögen es diese Situation auszuleben, die als Zwei-Personen-Spiel gespielt werden kann, indem sie versuchen, die Anzahl der Farben zu maximieren, die ihr Gegner braucht.
In einer anderen Variante der Karteneinfärbung, die als Empire-Färbung bekannt ist, beginnen wir mit zwei verschiedenen Karten auf zwei Blättern Papier mit der gleichen Anzahl an Ländern. Jedes Land auf einer der Karten (z. B. die Erde) wird mit genau einem Land auf der anderen Karte gepaart (das könnten Kolonien auf dem Mond sein).
Zusätzlich zu den üblichen Farbanforderungen verschiedener Farben für Länder, die eine Grenze teilen (für beide Karten), fügen wir die Anforderung hinzu, dass jedes Erdland genauso wie seine Kolonie auf dem Mond gefärbt sein muss. Wie viele Farben brauchen wir für dieses Problem? Die Antwort ist derzeit unbekannt.
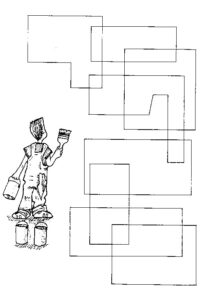
Die Lösung für Arbeitsblatt 4, unter Verwendung von nur zwei Farben (schattiert und weiß).