Arbeitsblatt: Der „Zaubertrick“
Vorführung
Dies ist deine Chance, ein Zauberer oder eine Zauberin zu sein!
Du brauchst einen Stapel von identischen, zweiseitigen Karten. (Um eigene Karten herzustellen, zerschneide ein großes Kartenblatt, das nur auf einer Seite gefärbt ist). Zur Vorführung ist es am einfachsten flache Magnetkarten zu verwenden, die auf jeder Seite anders gefärbt sind – Kühlschrankmagnete sind dafür ideal, wenn sie auf beiden Seiten magnetisch sind (viele davon sind es nur einseitig, dann klebe sie entsprechend aufeinander und markiere eine Seite mit einem weißen Punkt).
1. Bestimme eine Mitschülerin oder einen Mitschüler, die oder der 25 Karten als ein 5×5 Quadrat nach zufälliger, eigener Wahl an die Tafel heftet.
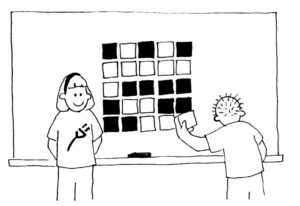
Nebenbei fügst du eine weitere Zeile und Spalte hinzu, „um die Sache schwieriger zu machen“.
Deine Karten sind aber der Trick dabei. Du musst die zusätzlichen Karten so auswählen, dass in jeder Zeile und Spalte eine gerade Anzahl von farbigen Karten vorhanden ist! Wähle ein Schulkind, das eine Karte umdrehen soll, während du deine Augen schließt und nicht zur Tafel gerichtet bist. Die Zeile und die Spalte, die die geänderte Karte enthält, hat nun eine ungerade Anzahl von farbigen Karten, und dies hilft die umgedrehte Karte zu identifizieren. Können die SchülerInnen erraten, wie der Trick funktioniert?
1. Jeweils zu zweit legen die SchülerInnen ihre Karten in einem 5×5 Quadrat aus.
2. Wie viele farbige Karten befinden sich in jeder Zeile und Spalte? Handelt es sich dabei um eine gerade oder ungerade Zahl? Beachte, ‘0’ wird als gerade Zahl betrachtet.
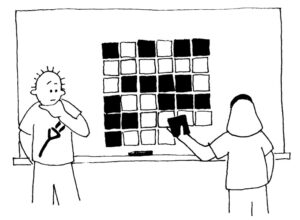
1. Füge jetzt jeder Reihe eine sechste Karte hinzu, sodass die Anzahl der farbigen Karten immer gerade ist. Die zusätzliche Karte wird als „paritätische“ Karte oder „Paritätskarte“ bezeichnet.
2. Füge anschließend ganz unten eine sechste Reihe hinzu, damit die Anzahl der farbigen Karten in jeder Spalte gerade ist.
3. Drehe jetzt eine Karte. Was fällt bei der betreffenden Zeile und Spalte auf?
(Beide haben eine ungerade Anzahl von farbigen Karten.) Paritätskarten werden benutzt, um anzuzeigen, wo ein Fehler aufgetreten ist.
4. Jetzt wechselt euch ab und führt den Trick aus.
1. Verwende andere Objekte. Alles, was zwei „Darstellungen“ hat, ist geeignet. Zum Beispiel könnten Spielkarten, Münzen (Kopf oder Zahl) oder Karten mit 0 oder 1 verwendet werden (um sich auf das binäre System zu beziehen).
2. Was passiert, wenn zwei oder mehr Karten umgedreht werden? (Es ist nicht immer möglich, genau zu wissen, welche beiden Karten umgedreht wurden, obwohl es möglich ist zu sagen, dass etwas geändert wurde. In der Regel kann man das Problem auf eine von zwei Kartenpaaren reduzieren. Bei vier Kartenumdrehungen ist es allerdings möglich, dass alle Paritätsbits korrekt sind und daher der Fehler unentdeckt bleibt!)
3. Versuche es mit einem größeren Feld, etwa ein 9×9 Quadrat, das mit der zusätzlichen Zeile und Spalte auf 10×10 erweitert wird. (Es wird für jede Feldgröße funktionieren und muss nicht quadratisch sein).
4. Eine weitere interessante Aufgabe ist, die Karte unten rechts zu betrachten. Wenn du sie als korrekten Wert für die Karten der Spalte darüber betrachtest, wird das auch für alle Karten in der Zeile links daneben gelten? (Ja, gilt immer für eine gerade Anzahl von Paritätsbits.) In dieser Aktivität haben wir gerade Parität mit einer geraden Anzahl von farbigen Karten verwendet. Können wir das auch für ungerader Parität verwenden? (Es ist möglich, aber die untere rechte Karte funktioniert nur für ihre Zeile und Spalte, wenn die Anzahl der Zeilen und Spalten beide gerade oder ungerade sind. Zum Beispiel funktioniert es bei den Anordnungen 5×9 oder 4×6, aber nicht bei 3×4.)
