Bevor das Aufgabenblatt verteilt wird, kann es sinnvoll sein das Prinzip vor der ganzen Gruppe zunächst einmal zu demonstrieren.
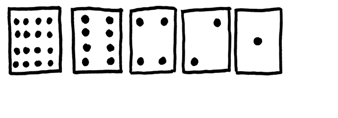
Für diese Aktivität benötigt die Lehrperson fünf Karten, welche (wie unten dargestellt) auf der einen Seite mit Punkten bedruckt sind, während sie auf der anderen Seite nicht bedruckt sind. Die Lehrperson beginnt damit fünf Kinder nach vorne zu bitten. Die Karten werden an die Kinder in der folgenden Reihenfolge verteilt:
Diskussion
Was fällt euch an der Anzahl der Punkte auf den Karten auf? (Jede Karte enthält jeweils doppelt so viele Punkte wie die vorherige Karte)
Wie viele Punkte müssten also auf der nächsten Karte auf der linken Seite sein, wenn wir noch eine Karte hinzunehmen würden? (32) und die darauf folgende…? (64)
Wir können diese Karten verwenden um Zahlen darzustellen, indem wir gewisse Karten drehen, sodass deren Punkte sichtbar sind (dies schreiben wir als 1), oder wir lassen sie, sodass keine Punkte sichtbar sind (wir schreiben eine 0). Wir zählen die Anzahl der sichtbaren Punkte. Frage die Kinder, wie man die Zahl 6 darstellen kann (4 Punkte und 2 Punkte), danach 15 (8, 4, 2 und 1 Punkt), danach 21 (16, 4 und 1).
Versuche nun die Klasse von null hochzählen zu lassen. Der Rest der Klasse soll sorgfältig zuschauen und versuchen das Muster zu erkennen. (Jede Karte dreht halb so oft wie die Karte rechts davon). Dies kann man mit mehr als nur einer Gruppe machen.
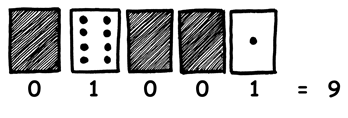
Fordere die Kinder auf die Zahl 01001 zu bilden. Welche Zahl wird dargestellt? (9). Wie sieht 17 als Binärzahl aus? (10001). Versuche noch einige Beispiele mehr, bis die Kinder das Konzept verstanden haben.
Nun gibt es fünf mögliche Aktivitäten, die folgen können, um das Konzept der Binärzahlen zu verstärken. Die Kinder sollten so viele davon erledigen, wie möglich.